Metric Area

These are the most common measurements of area (from smallest to largest):

• Square Millimeter
• Square Centimeter
• Square Meter
• Hectare
• Square Kilometer

Ariel the Dog is waiting patiently
inside 1 square meter.

Square Meter

The square meter is the basic unit of area of the Metric System.

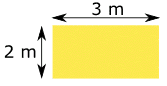
Area is length by length, so:

A square that is 1 meter on each side
is 1 square meter.

The Unit is meters × meters, which is written m² (square meters).

You could have other shapes (such as a rectangle that is ½ a meter by 2 meters) that also make 1 square meter.

Example: How big is this rectangle?

It is 2 meters by 3 meters, so it is 2 m × 3 m = 6 m²

congruent triangles

What is "Congruent" ... ?

It means that one shape can become another using Turns, Flips and/or Slides:

Rotation		Turn!
Reflection		Flip!
Translation		Slide!

Congruent Triangles

          When two triangles are congruent they will have exactly the same three sides and exactly the same three angles.
         The equal sides and angles may not be in the same position (if there is a turn or a flip), but they are there.

Solid Geometry

Solid Geometry is the geometry of three-dimensional space,
the kind of space we live in.

Three Dimensions

It is called three-dimensional, or 3D, because there are three dimensions: width, depth and height.

Simple Shapes

Let us start with some of the simplest shapes:

Common 3D Shapes

Properties

Solids have properties (special things about them), such as:

• volume (think of how much water it could hold)
• surface area (think of the area you would have to paint)
• how many vertices (corner points), faces and edges they have

                              ROGER  PENROSE

                    Sir Roger Penrose is widely considered one of the most important mathematical physicists of our time. His work on the properties of black holes, along with Stephen Hawking's, revolutionized our understanding of the nature of the universe.

WORKS OF PENROSE: 

                In the 1960s, working with Stephen Hawking, Penrose was able to prove that all matter within a black hole collapses into a single point, aka a singularity. According to Encyclopedia Britannica, this is "a geometric point in space where mass is compressed to infinite density and zero volume."
               Mass is so concentrated at this point of space that even light photons are unable to escape the black hole's maw.

 PENROSE  TRIANGLE:

                      In the 1950s Penrose, with his father, devised the Penrose triangle or impossible triangle/tribar.  Interestingly, the optical illusions appear to have first been developed by Oscar Reutersvärd in the 1930s. He was a Swedish graphic artist who has come to be known as the "father of the impossible figure". 

               ERIK  CHRISTOPHER  ZEEMAN

Zeeman's research has been in a variety of areas such as topology, in particular PL topology, dynamical systems and mathematical applications to biology and the social sciences. His initial research was in topology and one of his theorems was the unknotting of spheres in five dimensions. Certainly his work in topology would make him one of the leading topologists of all time but he may be known principally for other work.

Perhaps he is best known for his work on catastrophe theory for, although this theory was due initially to René Thom, it was Zeeman who brought it before the general public giving widespread publicity to applications of what was before that time thought of as pure mathematics. In particular Zeeman pioneered the applications of catastrophe theory in the biological and behavioural sciences, as well as the physical sciences.

Among the books which Zeeman has published are the texts Catastrophe theory (1977), Geometry and perspective (1987) and Gyroscopes and boomerangs (1989). One of his many memorable quotes, from his Catastrophe theory text, says much about mathematical philosophy:-

Technical skill is mastery of complexity while creativity is mastery of simplicity.

A shorter introduction to catastrophe theory than his 1977 book was given by Zeeman in his beautifully written survey article Bifurcation and catastrophe theory [Contemp. Math. (1981)]. The article introduces catastrophe theory in a unified way giving both elementary and non-elementary aspects. There is an elementary discussion of the cusp and the pitchfork and a statement of the classification theorem for elementary catastrophes. Asked what were the highlights of his own research he explained:-
 

In 1978, Zeeman gave the Christmas Lectures at the Royal Institution, out of which grew the Mathematics Master classes for 13-year old children that now flourishes in forty centres in the United Kingdom. He was the 63^rd President of the London Mathematical Society in 1986-88 and delivered the Presidential Address to the Society on 18 November 1988 On the classification of dynamical systems.

SYMMETRY OF SHAPES

Activity: Symmetry of Shapes

An Octagon

Let us try the Octagon (the 8-sided shape)

Is this a Line of Symmetry?

Let's try folding it:

Yes! When folded over, the edges match perfectly

So let us draw it on:

I found another way too::

Tried this	It works!

So let us draw it on, too:

In fact I found 8 Lines of Symmetry:

Annulus

An annulus is a flat shape like a ring. Its edges are two circles that have the same center.

The face of a metal washer is an annulus

Something shaped like an annulus is said to be annular.

Saturn has annular rings:

Area

Because it is a circle with a circular hole, you can calculate the area by subtracting the area of the "hole" from the big circle's area:

Area = πR² − πr²
= π( R² − r² )

Example: a steel pipe has an outside diameter (OD) of 100mm and an inside diameter (ID) of 80mm, what is the area of the cross section?

Convert diameter to radius for both outside and inside circles:

• R = 100 mm / 2 = 50 mm
• r = 80 mm / 2 = 40 mm

Now calculate area:

Area = π( R² - r² )

Area = 3.14159... × ( 50² − 40² )

Area = 3.14159... × (2500 − 1600)

Area = 3.14159... × 900

Area = 2827 mm² (to nearest mm²)